Порахувати кількість можливих комбінацій онлайн. Поєднання без повторень: Комбінаторика в MS EXCEL

Слід зазначити, що комбінаторика є самостійним розділом вищої математики (а не частиною тервера) і з цієї дисципліни написані важкі підручники, зміст яких часом анітрохи не легше абстрактної алгебри. Однак нам буде достатньо невеликої частки теоретичних знань, і в цій статті я постараюся у доступній формі розібрати основи теми з типовими комбінаторними завданнями. А багато хто з вас мені допоможуть;-)

Чим будемо займатися? У вузькому значенні комбінаторика - це підрахунок різних комбінацій, які можна скласти з деякої множини дискретнихоб'єктів. Під об'єктами розуміються якісь відокремлені предмети чи живі істоти – люди, звірі, гриби, рослини, комахи тощо. При цьому комбінаторику зовсім не хвилює, що безліч складається з тарілки манної каші, паяльника та болотяної жаби. Принципово важливо, що ці об'єкти піддаються перерахуванню – їх три (Дискретність)і суттєво те, що серед них немає однакових.

З безліччю розібралися, тепер про комбінації. Найпоширенішими видами комбінацій є перестановки об'єктів, їх вибірка з множини (поєднання) і розподіл (розміщення). Давайте прямо зараз подивимося, як це відбувається:

Перестановки, поєднання та розміщення без повторень

Не лякайтеся малозрозумілих термінів, тим більше деякі з них дійсно не дуже вдалі. Почнемо з хвоста заголовка – що означає « без повторень»? Це означає, що в даному параграфі будуть розглядатися множини, які складаються з різнихоб'єктів. Наприклад, … ні, кашу з паяльником і жабою пропонувати не буду, краще щось смачніше =) Уявіть, що перед вами на столі матеріалізувалося яблуко, груша і банан (за наявності таких ситуацію можна змоделювати і реально). Викладаємо фрукти зліва направо у такому порядку:

яблуко / груша / банан

Питання перше: Скільки способами їх можна переставити?

Одна комбінація вже записана вище та з іншими проблемами не виникає:

яблуко / банан / груша
груша / яблуко / банан
груша / банан / яблуко
банан / яблуко / груша
банан / груша / яблуко

Разом: 6 комбінацій або 6 перестановок.

Добре, тут не склало особливих труднощів перерахувати всі можливі випадки, але як бути, якщо предметів більше? Вже із чотирма різними фруктами кількість комбінацій значно зросте!

Будь ласка, відкрийте довідковий матеріал (методичку зручно роздрукувати)та у пункті № 2 знайдіть формулу кількості перестановок.

Жодних мук – 3 об'єкти можна переставити способами.

Питання друге: Скільки способами можна вибрати а) один фрукт, б) два фрукти, в) три фрукти, г) хоча б один фрукт?

Навіщо обирати? Так нагуляли апетит у попередньому пункті – для того, щоб з'їсти! =)

а) Один фрукт можна вибрати, очевидно, трьома способами - взяти або яблуко, грушу або банан. Формальний підрахунок проводиться за формулі кількості поєднань:

Запис у разі слід розуміти так: «скількими способами можна вибрати 1 фрукт з трьох?»

б) Перерахуємо всі можливі поєднання двох фруктів:

яблуко та груша;
яблуко та банан;
груші та банан.

Кількість комбінацій легко перевірити за тією самою формулою:

Запис розуміється аналогічно: «скільки можна вибрати 2 фрукти з трьох?».

в) І, нарешті, три фрукти можна вибрати єдиним способом:

До речі, формула кількості поєднань зберігає сенс і для порожньої вибірки:
способом можна вибрати жодного фрукта - власне, нічого не взяти і все.

г) Скільки способами можна взяти хоча б одинфрукт? Умова «хоча б один» передбачає, що нас влаштовує 1 фрукт (будь-який) або 2 будь-яких фрукти або всі 3 фрукти:
способами можна вибрати хоча б один фрукт.

Читачі, які уважно вивчили вступний урок з теорії ймовірностей, вже дещо здогадалися. Але про сенс знака "плюс" пізніше.

Для відповіді на наступне запитання мені потрібні два добровольці… …Ну що ж, якщо ніхто не хоче, тоді викликатиму до дошки =)

Питання третє: Скільки способами можна роздати по одному фрукту Даші та Наташі?

Для того, щоб роздати два фрукти, спочатку потрібно їх вибрати. Відповідно до пункту «бе» попереднього питання, зробити це можна засобами, перепишу їх заново:

яблуко та груша;
яблуко та банан;
груші та банан.

Але комбінацій зараз буде вдвічі більше. Розглянемо, наприклад, першу пару фруктів:
яблуком можна пригостити Дашу, а грушею – Наташу;
або навпаки – груша дістанеться Даші, а яблуко – Наталці.

І така перестановка можлива кожної пари фруктів.

Розглянемо ту саму студентську групу, яка пішла на танці. Скількими способами можна скласти пару з юнака та дівчини?

Способами можна вибрати 1 юнака;
способами можна вибрати 1 дівчину.

Таким чином, одного юнака іодну дівчину можна вибрати: методами.

Коли з кожної множини вибирається по 1 об'єкту, то справедливий наступний принцип підрахунку комбінацій: « коженоб'єкт з однієї множини може скласти пару з кожнимоб'єктом іншої множини».

Тобто Олег може запросити на танець будь-яку з 13 дівчат, Євген – теж будь-яку з тринадцяти, і аналогічний вибір має решта молодих людей. Разом: можливі пари.

Слід зазначити, що у цьому прикладі немає значення «історія» утворення пари; однак якщо взяти до уваги ініціативу, то кількість комбінацій треба подвоїти, оскільки кожна з 13 дівчат також може запросити на танець будь-якого юнака. Все залежить від умови того чи іншого завдання!

Схожий принцип справедливий і для складніших комбінацій, наприклад: скількома способами можна вибрати двох юнаків ідвох дівчат для участі у сценці КВК?

спілка Інедвозначно натякає, що комбінації необхідно перемножити:

Можливі групи артистів.

Іншими словами, кожнапара юнаків (45 унікальних пар) може виступати з будь-якийпарою дівчат (78 унікальних пар). А якщо розглянути розподіл ролей між учасниками, то комбінацій буде ще більше. …Дуже хочеться, але все-таки утримаюсь від продовження, щоб не прищепити вам огиду до студентського життя =).

Правило множення комбінацій поширюється і на більшу кількість множників:

Завдання 8

Скільки існує трицифрових чисел, які діляться на 5?

Рішення: для наочності позначимо це число трьома зірочками: ***

У розряд сотеньможна записати будь-яку з цифр (1, 2, 3, 4, 5, 6, 7, 8 чи 9). Нуль не годиться, тому що в цьому випадку число перестає бути тризначним.

А ось у розряд десятків(«посередині») можна вибрати будь-яку з 10 цифр: .

За умовою, число має ділитися на 5. Число ділиться на 5, якщо воно закінчується на 5 або на 0. Таким чином, у молодшому розряді нас влаштовують 2 цифри.

Отже, існує: трицифрових чисел, які діляться на 5.

При цьому твір розшифровується так: «9 способами можна вибрати цифру в розряд сотень і 10 способами вибрати цифру в розряд десятків і 2 способами в розряд одиниць»

Або ще простіше: « кожназ 9 цифр у розряді сотенькомбінується з кожноюз 10 цифр розряду десятків і з кожноюз двох цифр у розряд одиниць».

Відповідь: 180

А зараз…

Так, мало не забув про обіцяний коментар до завдання № 5, в якому Борі, Дімі та Володі можна здати за однією картою способами. Множення тут має той самий сенс: способами можна витягти 3 карти з колоди І в кожнійвибірці переставити їх засобами.

А тепер завдання для самостійного вирішення… зараз придумаю щось цікавіше, …нехай буде про ту ж російську версію блекджека:

Завдання 9

Скільки існує виграшних комбінацій з 2 карток при грі в «очко»?

Для тих, хто не знає: виграє комбінація 10 + ТУЗ (11 очок) = 21 очко і, давайте вважатимемо виграшною комбінацію з двох тузів.

(Порядок карт у будь-якій парі не має значення)

Коротке рішення та відповідь наприкінці уроку.

До речі, не слід вважати приклад примітивним. Блекджек - це чи не єдина гра, для якої існує математично обґрунтований алгоритм, що дозволяє вигравати у казино. Бажаючі можуть легко знайти масу інформації про оптимальну стратегію та тактику. Щоправда, такі майстри досить швидко потрапляють до чорного списку всіх закладів.

Настав час закріпити пройдений матеріал парою солідних завдань:

Завдання 10

У Васі вдома живуть 4 коти.

а) скільки можна розсадити котів по кутах кімнати?
б) скільки можна відпустити гуляти котів?
в) Скільки способами Вася може взяти на руки двох котів (одного на ліву, іншого - на праву)?

Вирішуємо: по-перше, знову слід звернути увагу на те, що в задачі йдеться про різнихоб'єктах (навіть якщо коти – однояйцеві близнюки). Це дуже важлива умова!

а) Мовчання котів. Цю кару зазнають відразу всі коти
+ важливе їх розташування, тому тут мають місце перестановки:
способами можна розсадити котів по кутах кімнати.

Повторюся, що з перестановках має значення лише кількість різних об'єктів та його взаємне розташування. Залежно від настрою Вася може розсаджувати тварин півколом на дивані, ряд на підвіконні і т.д. – перестановок у всіх випадках буде 24. Бажаючі можуть для зручності уявити, що коти різнокольорові (наприклад, білий, чорний, рудий та смугастий) та перерахувати всі можливі комбінації.

б) Скільки можна відпустити гуляти котів?

Передбачається, що коти ходять гуляти тільки через двері, при цьому питання має на увазі байдужість щодо кількості тварин – на прогулянку можуть вийти 1, 2, 3 або всі 4 коти.

Вважаємо всі можливі комбінації:

Способами можна відпустити гуляти одного кота (будь-якого з чотирьох);
способами можна відпустити гуляти двох котів (варіанти перерахуйте самостійно);
способами можна відпустити гуляти трьох котів (якийсь один із чотирьох сидить удома);
способом можна випустити всіх котів.

Напевно, ви здогадалися, що отримані значення слід підсумувати:
способами можна відпустити гуляти котів.

Ентузіастам пропоную ускладнену версію завдання – коли будь-який кіт у будь-якій вибірці випадково може вийти на вулицю як через двері, так і через вікно 10 поверху. Комбінацій помітно побільшає!

в) Скільки способами Вася може взяти на руки двох котів?

Ситуація передбачає не тільки вибір 2 тварин, а й їх розміщення по руках:
способами можна взяти на руки 2 коти.

Другий варіант вирішення: способами можна вибрати двох котів іспособами посадити кожнупару на руки:

Відповідь: а) 24, б) 15, в) 12

Ну і для очищення совісті щось конкретніше на збільшення комбінацій. Нехай у Васі додатково живе 5 котів =) Скільки способами можна відпустити гуляти 2 котів і 1 кішку?

Тобто, з кожноюпарою котів можна випустити кожнукішку.

Ще один баян для самостійного вирішення:

Завдання 11

У ліфт 12-поверхового будинку сіли 3 пасажири. Кожен, незалежно від інших, з однаковою ймовірністю може вийти на будь-якому (починаючи з 2-го) поверсі. Скількими способами:

1) пасажири можуть вийти на тому самому поверсі (Порядок виходу не має значення);
2) дві людини можуть вийти на одному поверсі, а третя – на іншому;
3) люди можуть вийти різних поверхах;
4) пасажири можуть вийти із ліфта?

І тут часто перепитують, уточнюю: якщо 2 чи 3 особи виходять на одному поверсі, то черговість виходу не має значення. ДУМАЙТЕ, використовуйте формули та правила додавання/множення комбінацій. У разі труднощів пасажирам корисно дати імена та поміркувати, у яких комбінаціях вони можуть вийти з ліфта. Не треба засмучуватися, якщо щось не вийде, наприклад, пункт № 2 досить підступний.

Повне рішення із докладними коментарями наприкінці уроку.

Заключний параграф присвячений комбінаціям, які теж зустрічаються досить часто – за моєю суб'єктивною оцінкою, приблизно 20-30% комбінаторних завдань:

Перестановки, поєднання та розміщення з повтореннями

Перелічені види комбінацій законспектовані у пункті № 5 довідкового матеріалу Основні формули комбінаторикиПроте деякі з них за першим прочитанням можуть бути не дуже зрозумілими. І тут спочатку доцільно ознайомитися з практичними прикладами, і лише потім осмислювати загальне формулювання. Поїхали:

Перестановки із повтореннями

У перестановках із повтореннями, як і в «звичайних» перестановках, бере участь відразу все безліч об'єктів, але є одне але: в даному множині один або більша кількість елементів (об'єктів) повторюються. Зустрічайте черговий стандарт:

Завдання 12

Скільки різних буквосполучень можна отримати перестановкою карток із наступними літерами: К, О, Л, О, К, О, Л, Ь, Ч, І, К?

Рішення: у тому випадку, якби всі літери були різні, то слід було б застосувати тривіальну формулу , проте цілком зрозуміло, що для запропонованого набору карток деякі маніпуляції спрацьовуватимуть «вхолосту», наприклад, якщо поміняти місцями будь-які дві картки з літерами «К » у будь-якому слові, то вийде те саме слово. Причому фізично картки можуть сильно відрізнятися: одна бути круглою з надрукованою літерою «К», інша – квадратною з намальованою літерою «К». Але за змістом завдання навіть такі картки вважаються однаковими, оскільки в умові питається про буквосполучення.

Все дуже просто – всього: 11 карток, серед яких літера:

К - повторюється 3 рази;
Про - повторюється 3 рази;
Л – повторюється двічі;
Ь - повторюється 1 раз;
Ч – повторюється 1 раз;
І – повторюється один раз.

Перевірка: 3 + 3 + 2 + 1 + 1 + 1 = 11, що потрібно перевірити.

За формулою кількості перестановок із повтореннями:
різних буквосполучень можна отримати. Більше півмільйона!

Для швидкого розрахунку великого факторіального значення зручно використовувати стандартну функцію Екселю: забиваємо в будь-яку комірку =ФАКТР(11)і тиснемо Enter.

На практиці цілком допустимо не записувати загальну формулу і, крім того, опускати поодинокі факторіали:

Але попередні коментарі про літери, що повторюються, обов'язкові!

Відповідь: 554400

Інший типовий приклад перестановок з повтореннями зустрічається в задачі про розміщення шахових фігур, яку можна знайти на складі готових рішеньу відповідній pdf-ці. А для самостійного рішення я вигадав менш шаблонне завдання:

Завдання 13

Олексій займається спортом, причому 4 дні на тиждень – легкою атлетикою, 2 дні – силовими вправами та 1 день відпочиває. Скільки способами він може скласти собі розклад занять на тиждень?

Формула тут не годиться, оскільки враховує збігаються перестановки (наприклад, коли міняються місцями силові вправи у середу із силовими вправами у четвер). І знову - за фактом ті ж 2 силові тренування можуть сильно відрізнятися один від одного, але за контекстом завдання (з точки зору розкладу) вони вважаються однаковими елементами.

Дворядкове рішення та відповідь наприкінці уроку.

Поєднання з повтореннями

Характерна риса цього виду комбінацій у тому, що вибірка проводиться із кількох груп, кожна у тому числі складається з однакових об'єктів.

Сьогодні всі добре попрацювали, тому настав час підкріпитись:

Завдання 14

У студентській їдальні продають сосиски в тесті, ватрушки та пончики. Скільки можна придбати п'ять пиріжків?

Рішення: відразу зверніть увагу на типовий критерій поєднань із повтореннями – за умовою на вибір запропоновано не безліч об'єктів як таке, а різні видиоб'єктів; при цьому передбачається, що у продажу є не менше п'яти хот-догів, 5 ватрушок та 5 пончиків. Тістечка в кожній групі, зрозуміло, відрізняються - бо абсолютно ідентичні пончики можна змоделювати хіба що на комп'ютері =) Проте фізичні характеристики пиріжків за змістом завдання не суттєві, і хот-доги/ватрушки/пончики у своїх групах вважаються однаковими.

Що може бути у вибірці? Насамперед, слід зазначити, що у вибірці обов'язково будуть однакові пиріжки (обираємо 5 штук, а на вибір запропоновано 3 види). Варіанти тут на будь-який смак: 5 хот-догів, 5 ватрушок, 5 пончиків, 3 хот-доги + 2 ватрушки, 1 хот-дог + 2 + ватрушки + 2 пончики і т.д.

Як і при «звичайних» поєднаннях, порядок вибору та розміщення пиріжків у вибірці не має значення – просто вибрали 5 штук та все.

Використовуємо формулу кількості поєднань із повтореннями:
способом можна придбати 5 пиріжків.

Смачного!

Відповідь: 21

Який висновок можна зробити із багатьох комбінаторних завдань?

Іноді найважче – це розібратися в умові.

Аналогічний приклад для самостійного вирішення:

Завдання 15

У гаманці знаходиться досить велика кількість 1-, 2-, 5- та 10-рублевих монет. Скільки способами можна витягти три монети з гаманця?

З метою самоконтролю дайте відповідь на кілька простих питань:

1) Чи можуть у вибірці всі монети бути різними?
2) Назвіть найдешевшу і найдорожчу комбінацію монет.

Рішення та відповіді наприкінці уроку.

З мого особистого досвіду, можу сказати, що поєднання з повтореннями – найрідкісніший гість на практиці, чого не скажеш про такий вид комбінацій:

Розміщення з повтореннями

З множини, що складається з елементів, вибирається елементів, при цьому важливий порядок елементів у кожній вибірці. І все було б нічого, але досить несподіваний прикол полягає в тому, що будь-який об'єкт вихідної множини ми можемо вибирати скільки завгодно разів. Образно кажучи, від «багато не убуде».

Коли таке буває? Типовим прикладом є кодовий замок з кількома дисками, але через розвиток технологій актуальніше розглянути його цифрового нащадка:

Завдання 16

Скільки існує чотиризначних пін-кодів?

Рішення: насправді для розрулювання завдання достатньо знань правил комбінаторики: способами можна вибрати першу цифру пін-коду іспособами – другу цифру пін-коду істільки ж способами – третю істільки ж – четверту. Таким чином, за правилом множення комбінацій, чотиризначний пін-код можна скласти: способами.

А тепер за допомогою формули. За умовою нам запропоновано набір із цифр, з якого вибираються цифри та розташовуються у визначеному порядку, при цьому цифри у вибірці можуть повторюватися (тобто будь-якою цифрою вихідного набору можна користуватися довільну кількість разів). За формулою кількості розміщень із повтореннями:

Відповідь: 10000

Що тут спадає на думку… …якщо банкомат «з'їдає» картку після третьої невдалої спроби введення пін-коду, то шанси підібрати його навмання дуже примарні.

І хто сказав, що у комбінаториці немає жодного практичного сенсу? Пізнавальне завдання для всіх читачів сайт:

Завдання 17

Згідно з державним стандартом, автомобільний номерний знак складається з 3 цифр та 3 літер. При цьому неприпустимий номер із трьома нулями, а літери вибираються з набору А, В, Е, К, М, Н, О, Р, С, Т, У, Х (використовуються лише ті літери кирилиці, написання яких збігається з латинськими літерами).

Скільки номерних знаків можна скласти для регіону?

Не так їх, до речі, багато. У великих регіонах такої кількості не вистачає, і тому для них існує кілька кодів до напису RUS.

Рішення та відповідь наприкінці уроку. Не забуваємо використовувати правила комбінаторики;-) …Хотів похвалитися ексклюзивом, та виявилося не ексклюзивом =) Заглянув у Вікіпедію – там є розрахунки, щоправда, без коментарів. Хоча у навчальних цілях, напевно, мало хто вирішував.

Наше захоплююче заняття добігло кінця, і насамкінець я хочу сказати, що ви не дарма витратили час – з тієї причини, що формули комбінаторики знаходять ще одне насущне практичне застосування: вони зустрічаються в різних завданнях теорії ймовірностей,
і в завдання на класичне визначення ймовірності- Особливо часто =)

Дякую всім за активну участь і до швидких зустрічей!

Рішення та відповіді:

Завдання 2: Рішення: знайдемо кількість всіх можливих перестановок 4 карток:

Коли картка з нулем розташовується на 1-му місці, то число стає тризначним, тому ці комбінації слід виключити. Нехай нуль знаходиться на 1-му місці, тоді 3 цифри, що залишилися, в молодших розрядах можна переставити способами.

Примітка : т.к. карток небагато, то тут нескладно перерахувати всі такі варіанти:
0579
0597
0759
0795
0957
0975

Таким чином, із запропонованого набору можна скласти:
24 - 6 = 18 чотиризначних чисел
Відповідь : 18

Завдання 4: Рішення: способами можна вибрати 3 карти з 36
Відповідь : 7140

Завдання 6: Рішення: методами.
Інший варіант вирішення : способами можна вибрати двох осіб з групи та
2) «Найдешевший» набір містить 3 рублеві монети, а «найдорожчий» – 3 десятирублеві.

Завдання 17: Рішення: способами можна скласти цифрову комбінацію автомобільного номера, причому одну з них (000) слід виключити: .
способами можна скласти літерну комбінацію автомобільного номера.
За правилом множення комбінацій, всього можна скласти:
автомобільних номерів
(кожнацифрова комбінація поєднується з кожноюлітерною комбінацією).
Відповідь : 1726272

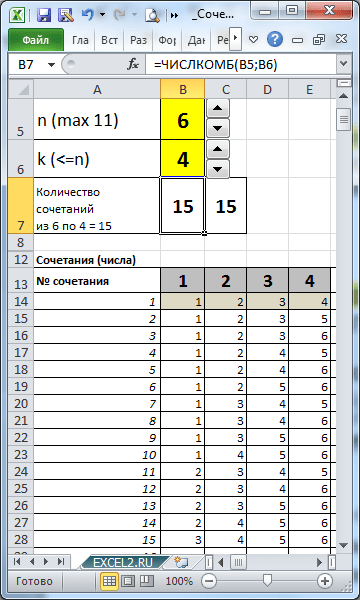
Підрахуємо в MS EXCEL кількість поєднань із n елементів по k. За допомогою формул виведемо на аркуш всі варіанти поєднань (англійський переклад терміна: Combinations without repetition).

Поєднаннями з n різних елементів до k елементів називаються комбінації, які відрізняються хоча б одним елементом. Наприклад, нижче перераховані ВСІ 3-х елементні поєднання, взяті з множини, що складається з 5 елементів (1; 2; 3; 4; 5):

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примітка: Це стаття про підрахунок кількості поєднань з використанням MS EXCEL Теоретичні основи радимо прочитати у спеціалізованому підручнику. Вивчати поєднання за цією статтею – погана ідея.

Відмінність Поєднань від Розміщень

Виведення всіх комбінацій Поєднань

У прикладному файлі створені формули для виведення всіх Поєднань для заданих n і k.

Задаючи за допомогою кількість елементів множини (n) і кількість елементів, яку ми вибираємо з нього (k), за допомогою формул можна вивести всі Поєднання.

Завдання

Автовоз може перевозити по 4 легкові машини. Необхідно перевезти 7 різних машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Скільки різними способами можна заповнити перший автовоз? Конкретне місце машини в автовозі не має значення.

Нам потрібно визначити число Поєднань 7 машин на 4-х місцях автовозу. Тобто. n=7, а k=4. Виявляється, що таких варіантів = ЧИСЛКОМБ (7; 4) дорівнює 35.

Комбінаторика - це розділ математики, у якому вивчаються питання, скільки різних комбінацій, підпорядкованих тим чи іншим умовам, можна скласти із заданих об'єктів. Основи комбінаторики дуже важливі з метою оцінки ймовірностей випадкових подій, т.к. саме вони дозволяють підрахувати принципово можливу кількість різних варіантів розвитку подій.

Основна формула комбінаторики

Нехай є k груп елементів, причому i група складається з n i елементів. Виберемо по одному елементу з кожної групи. Тоді загальна кількість N способів, якими можна зробити такий вибір, визначається співвідношенням N = n 1 * n 2 * n 3 * ... * n k .

приклад 1.Пояснимо це правило простому прикладі. Нехай є дві групи елементів, причому перша група складається з n 1 елементів, а друга - n 2 елементів. Скільки різних пар елементів можна скласти із цих двох груп, таким чином, щоб у парі було по одному елементу від кожної групи? Допустимо, ми взяли перший елемент із першої групи і, не змінюючи його, перебрали всі можливі пари, змінюючи лише елементи з другої групи. Таких пар цього елемента можна скласти n 2 . Потім ми беремо другий елемент із першої групи і також складаємо для нього всі можливі пари. Таких пар також буде n 2 . Так як у першій групі всього n 1 елемент, всього можливих варіантів буде n 1 * n 2 .

приклад 2.Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?
Рішення: n 1 =6 (т.к. як перша цифра можна взяти будь-яку цифру з 1, 2, 3, 4, 5, 6), n 2 =7 (т.к. як другу цифру можна взяти будь-яку цифру з 0 , 1, 2, 3, 4, 5, 6), n 3 =4 (т.к. як третя цифра можна взяти будь-яку цифру з 0, 2, 4, 6).
Отже, N = n 1 * n 2 * n 3 = 6 * 7 * 4 = 168.

У разі, коли всі групи складаються з однакового числа елементів, тобто. n 1 =n 2 =...n k =n вважатимуться, кожен вибір виробляється з однієї й тієї групи, причому елемент після вибору знову повертається у групу. Тоді число всіх способів вибору дорівнює n k. Такий спосіб вибору комбінаторики носить назву вибірки із поверненням.

приклад 3.Скільки всіх чотирицифрових чисел можна становити з цифр 1, 5, 6, 7, 8?
Рішення.До кожного розряду чотиризначного числа є п'ять можливостей, отже N=5*5*5*5=5 4 =625.

Розглянемо безліч, які з n елементів. Це безліч у комбінаториці називається генеральною сукупністю.

Число розміщень з n елементів m

Визначення 1.Розміщенням з nелементів по mу комбінаториці називається будь-який упорядкований набірз mрізних елементів, вибраних з генеральної сукупності в nелементів.

приклад 4.Різними розміщеннями з трьох елементів (1, 2, 3) по два будуть набори (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2) ). Розміщення можуть відрізнятися друг від друга як елементами, і їх порядком.

Число розміщень у комбінаториці позначається A n m і обчислюється за такою формулою:

Примітка: n!=1*2*3*...*n (читається: "ен факторіал"), крім того вважають, що 0!=1.

Приклад 5. Скільки існує двозначних чисел, у яких цифра десятків та цифра одиниць різні та непарні?
Рішення:т.к. непарних цифр п'ять, саме 1, 3, 5, 7, 9, це завдання зводиться до вибору і розміщення дві різні позиції двох із п'яти різних цифр, тобто. вказаних чисел буде:

Визначення 2. Поєднаннямз nелементів по mу комбінаториці називається будь-який невпорядкований набірз mрізних елементів, вибраних з генеральної сукупності в nелементів.

Приклад 6. Для множини (1, 2, 3) поєднаннями є (1, 2), (1, 3), (2, 3).

Число поєднань з n елементів m

Число поєднань позначається C n m і обчислюється за такою формулою:

Приклад 7.Скільки способами читач може вибрати дві книжки із шести наявних?

Рішення:Число методів дорівнює числу поєднань із шести книжок по дві, тобто. одно:

Перестановки з n елементів

Визначення 3. Перестановкоюз nелементів називається будь-який упорядкований набірцих елементів.

Приклад 7a.Різними перестановками множини, що складається з трьох елементів (1, 2, 3) є: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), ( 3, 2, 1), (3, 1, 2).

Число різних перестановок з елементів n позначається P n і обчислюється за формулою P n = n!.

Приклад 8.Скільки способами сім книг різних авторів можна розставити на полиці в один ряд?

Рішення:це завдання про кількість перестановок семи різних книг. Є P 7 =7!=1*2*3*4*5*6*7=5040 способів здійснити розміщення книг.

Обговорення. p align="justify"> Ми бачимо, що число можливих комбінацій можна порахувати за різними правилами (перестановки, поєднання, розміщення) причому результат вийде різний, т.к. Принцип підрахунку і самі формули відрізняються. Уважно подивившись визначення, можна побачити, що результат залежить від кількох чинників одночасно.

По-перше, з того, з якої кількості елементів ми можемо комбінувати їх набори (наскільки велика генеральна сукупність елементів).

По-друге, результат залежить від того, який розмір набори елементів нам потрібні.

І останнє, важливо знати, чи є для нас суттєвим порядок елементів у наборі. Пояснимо останній чинник на такому прикладі.

Приклад 9.На батьківських зборах присутні 20 осіб. Скільки існує різних варіантів складу батьківського комітету, якщо до нього мають увійти 5 осіб?
Рішення:У цьому прикладі нас не цікавить порядок прізвищ у списку Комітету. Якщо в результаті в його складі будуть одні й ті ж люди, то за змістом для нас це один і той самий варіант. Тому ми можемо скористатися формулою для підрахунку числа поєднаньіз 20 елементів по 5.

Інакше будуть справи, якщо кожен член комітету спочатку відповідає за певний напрямок роботи. Тоді при тому самому списковому складі комітету, всередині нього можливо 5! варіантів перестановокякі мають значення. Кількість різних (і за складом, і за сферою відповідальності) варіантів визначається у цьому випадку числом розміщеньіз 20 елементів по 5.

Завдання для самоперевірки
1. Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?

2. Скільки існує п'ятизначних чисел, які однаково читаються зліва направо та праворуч наліво?

3. У класі десять предметів та п'ять уроків на день. Скільки способами можна скласти розклад на один день?

4. Скільки можна вибрати 4 делегати на конференцію, якщо в групі 20 осіб?

5. Скільки способами можна розкласти вісім різних листів по восьми різних конвертах, якщо кожен конверт кладеться лише одне лист?

6. З трьох математиків та десяти економістів треба скласти комісію, що складається з двох математиків та шести економістів. Скільки способами це можна зробити?

Ми іноді робимо вибір із безлічі без урахування порядку. Такий вибір називається комбінацією . Якщо ви граєте в карти, наприклад, ви знаєте, що в більшості ситуацій порядок, у якому ви тримаєте карти, не має значення.

Приклад 1Знайдіть усі комбінації 3-х букв, взятих із набору в 5 букв (A, B, C, D, E).

РішенняЦі комбінації такі:
(A, B, C), (A, B, D),
(A, B, E), (A, C, D),
(A, C, E), (A, D, E),
(B, C, D), (B, C, E),
(B, D, E), (C, D, E).
Існує 10 комбінацій із трьох букв, вибраних із п'яти букв.

Коли ми знаходимо всі комбінації з набору з 5 об'єктами, якщо ми беремо 3 об'єкти за один раз, ми знаходимо всі 3-елементні підмножини. У разі порядок об'єктів не розглядається. Тоді,
(A, C, B) називається одним і тим же набором як і (A, B, C).

Підмножина
Множина A є підмножиною B, і означає, що A це підмножина та/або збігається з B якщо кожен елемент A є елементом B.

Елементи підмножини не впорядковані. Коли розглядаються комбінації, розглядається порядок!

Комбінація
Комбінація, що містить k об'єктів є підмножиною, що складається з k об'єктів.

Ми хочемо записати формулу для обчислення число поєднань із n об'єктів, якщо взято до об'єктів одночасно.

Позначення комбінації
Число поєднань з n об'єктів, якщо взято до об'єктів одночасно, позначається n C k .

Ми називаємо n C k кількість поєднань . Ми хочемо записати загальну формулу для n C k для будь-якого k ≤ n. По-перше, це вірно, що n C n = 1, тому що безліч з n елементами має тільки одне підмножина з n елементами, є сама безліч. По-друге, n C 1 = n, тому що множина з n елементами має тільки n підмножин з 1 елементом у кожному. Нарешті, n C 0 = 1, тому що множина з n елементами має тільки одну підмножину з 0 елементами, тобто пусту множину ∅. Щоб розглянути інші поєднання, повернімося до прикладу 1 і порівняємо кількість комбінацій з кількістю перестановок.

Зауважте, що кожна комбінація з 3-х елементів має 6, або 3!, перестановок.
3! . 5 C 3 = 60 = 5 P 3 = 5. 4 . 3,
so
.
Загалом, число поєднань з k елементів, вибраних з n об'єктів, n C k разів перестановок цих елементів k!, Повинне дорівнювати числу перестановок n елементів по k елементів:
k! n C k = n P k
n C k = n P k /k!
n C k = (1/k!). n P k
n C k =

Комбінації k об'єктів з n об'єктів
Загальна кількість комбінацій до елементів з об'єктів n позначається n C k , визначається
(1) n C k = ,
або
(2) n C k =

Інший тип позначення для n C k це біномінальний коефіцієнт . Причина для такої термінології буде зрозумілою нижче.

Біномінальний коефіцієнт

Приклад 2Обчисліть , використовуючи формули (1) та (2).

Рішення
a) Відповідно до (1),
.
b) Відповідно до (2),

Майте на увазі, що не означає n/k.

Приклад 3Обчисліть та .

РішенняМи використовуємо формулу (1) для першого виразу та формулу (2) для другого. Тоді
,
використовуючи (1), та
,
використовуючи формулу (2).

Зверніть увагу, що
,
та використовуючи результат прикладу 2 дає нам
.
Звідси випливає, що число 5-ти елементного підмножини з множини 7 елементів те саме, що і число 2-елементного підмножини множини з 7 елементів. Коли 5 елементів вибираються з набору, вони не включають 2 елементи. Щоб побачити це, розглянемо безліч (A, B, C, D, E, F, G):


Загалом, ми маємо таке. Цей результат дає альтернативний спосіб обчислення комбінації.

Підмножини розміру k та розміру
і n C k = n C n-k
Число підмножин розміру до множини з n об'єктами таке ж, як і число підмножин розміру n - до.

Тепер ми вирішуватимемо завдання з комбінаціями.

Приклад 4 Мічиганська лотерея. Лотерея WINFALL, що проводиться в штаті Мічиган двічі на тиждень, має джек-пот, який, принаймні, дорівнює 2 млн. доларів США. За один долар гравець може закреслити будь-які 6 чисел від 1 до 49. Якщо ці числа збігаються з тими, що випадають під час проведення лотереї, гравець виграє. (