itthon · Székrekedés · Az első típusú nem megfelelő integrálok. Hogyan lehet kiszámítani egy nem megfelelő integrált és megtudni a konvergenciáját? 2. típusú helytelen integrál online

Az első típusú nem megfelelő integrálok. Hogyan lehet kiszámítani egy nem megfelelő integrált és megtudni a konvergenciáját? 2. típusú helytelen integrál online

Az első típusú nem megfelelő integrálok. Lényegében ez ugyanaz a határozott integrál, de azokban az esetekben, amikor az integráloknak végtelen felső vagy alsó integrációs határa van, vagy mindkét integrálási határ végtelen.

A második típusú nem megfelelő integrálok. Lényegében ez ugyanaz a határozott integrál, de azokban az esetekben, amikor az integrált korlátlan függvényekből vesszük, a véges számú pontban lévő integrandusnak nincs véges integrálási szegmense, amely végtelenbe fordul.

Összehasonlításképp. A határozott integrál fogalmának bevezetésekor azt feltételeztük, hogy a függvény f(x) folyamatos a [ a, b], és az integrációs szegmens véges, azaz számok korlátozzák, és nem a végtelen. Egyes feladatok e korlátozások feladásához vezetnek. Így jelennek meg a nem megfelelő integrálok.

A nem megfelelő integrál geometriai jelentése Egészen egyszerűen kiderül. Abban az esetben, ha egy függvény grafikonja y = f(x) a tengely felett van Ökör, a határozott integrál egy görbével határolt görbe vonalú trapéz területét fejezi ki y = f(x) , x tengely és ordináták x = a , x = b. A nem megfelelő integrál viszont egy korlátlan (végtelen) görbe vonalú trapéz területét fejezi ki, amely a vonalak közé van zárva y = f(x) (az alábbi képen - piros), x = aés az abszcissza tengely.

A helytelen integrálokat hasonlóképpen határozzuk meg más végtelen intervallumokhoz:

Egy végtelen görbe trapéz területe lehet véges szám, ebben az esetben a nem megfelelő integrált konvergensnek nevezzük. A terület lehet végtelen is, és ebben az esetben a nem megfelelő integrált divergensnek nevezzük.

Egy integrál határértékének használata a nem megfelelő integrál helyett. A nem megfelelő integrál kiértékeléséhez a határozott integrál határértékét kell használni. Ha ez a határ létezik, és véges (nem egyenlő a végtelennel), akkor a nem megfelelő integrált konvergensnek, egyébként pedig divergensnek nevezzük. Az, hogy egy változó milyen mértékben hajlik a határjel alá, attól függ, hogy az első vagy a második típusú nem megfelelő integrállal van-e dolgunk. Ezt most derítsük ki.

Az első típusú helytelen integrálok - végtelen korlátokkal és konvergenciájukkal

Nem megfelelő integrálok végtelen felső határral

Tehát egy nem megfelelő integrál írása abban különbözik a szokásos határozott integráltól, hogy az integráció felső határa végtelen.

Meghatározás. Nem megfelelő integrál egy folytonos függvény integrálásának végtelen felső határával f(x) közötti intervallumban a előtt ∞ ennek a függvénynek az integráljának határát az integráció felső határával nevezzük b és az integráció alsó határa a feltéve, hogy az integráció felső határa korlátlanul nő, azaz

.

Ha ez a határ létezik, és nem a végtelen, hanem valamilyen számmal egyenlő, akkor a nem megfelelő integrált konvergensnek nevezzük, és azt a számot veszik értéknek, amellyel a határ egyenlő. Másképp a nem megfelelő integrált divergensnek nevezzükés semmi értelmet nem tulajdonítanak neki.

Példa 1. Számítsa ki a nem megfelelő integrált(ha összefolyik).

Megoldás. A nem megfelelő integrál definíciója alapján azt találjuk

Mivel a határ létezik és egyenlő 1-gyel, akkor ez helytelen integrál konvergálés egyenlő 1-gyel.

A következő példában az integrandus majdnem ugyanaz, mint az 1. példában, csak az x fok nem kettő, hanem az alfa betű, és a feladat a nem megfelelő integrál tanulmányozása a konvergenciához. Vagyis a kérdés megválaszolásra vár: milyen alfa-értékeknél konvergál ez a helytelen integrál, és milyen értékeknél tér el?

2. példa Vizsgálja meg a nem megfelelő integrált a konvergenciára(az integráció alsó határa nagyobb, mint nulla).

Megoldás. Akkor először tegyük fel, hogy

Az eredményül kapott kifejezésben a következő határértékre lépünk:

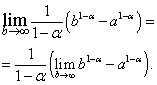
Könnyen belátható, hogy a jobb oldali határérték létezik, és egyenlő nullával, amikor, azaz, és nem létezik, amikor, azaz.

Az első esetben, amikor . Ha akkor és nem létezik.

Tanulmányunk következtetése a következő: ez helytelen integrál konvergálés eltér nál nél .

A Newton-Leibniz képlet alkalmazása a vizsgált nem megfelelő integrál típusára , levezetheti a következő képletet, amely nagyon hasonlít hozzá:

.

Ez egy általánosított Newton-Leibniz képlet.

3. példa: Számítsa ki a nem megfelelő integrált(ha összefolyik).

Ennek az integrálnak a határa létezik:

A második integrál, amely az eredeti integrált kifejező összeget alkotja:

Ennek az integrálnak a határa is létezik:

.

Megtaláljuk két integrál összegét, ami egyben az eredeti nem megfelelő integrál értéke is két végtelen határral:

A második típusú helytelen integrálok - korlátlan függvényekből és konvergenciájukból

Legyen a függvény f(x) tól származó szegmensen megadva a előtt b és korlátlan. Tegyük fel, hogy a függvény a pontban a végtelenbe megy b , míg a szakasz összes többi pontján folytonos.

Meghatározás. Egy függvény nem megfelelő integrálja f(x) től származó szegmensen a előtt b ennek a függvénynek az integráljának határát az integráció felső határával nevezzük c , ha a törekvés során c Nak nek b a függvény korlátozás nélkül növekszik, és a ponton x = b funkció nincs definiálva, azaz

.

Ha ez a határ létezik, akkor a második típusú nem megfelelő integrált konvergensnek, ellenkező esetben divergensnek nevezzük.

A Newton-Leibniz képlet segítségével levezetjük.

1. Második típusú nem megfelelő integrál definíciója

Hadd f(x) értéke [ a;b], de korlátlan. Hagyjuk a határozottság kedvéért f(x) határtalan a pont bal szomszédságában b: , de a függvény bármely intervallumban integrálható. Ebben az esetben a lényeg b hívott speciális pont.

Meghatározás. A második típusú nem megfelelő integrál funkciókat f(x) tovább [ a;b] az at integrál véges vagy végtelen határának nevezzük

Ha létezik (1) határérték és véges, akkor azt mondjuk, hogy az integrál konvergál, és a határértéket tekintjük az integrál értékének. Ha az (1) határ nem létezik, vagy egyenlő a végtelennel, akkor az integrálról azt mondjuk, hogy divergál.

Hasonlóképpen definiáljuk a függvény integrálját is f(x), korlátlan a pont jobb szomszédságában A:

1. példa Vizsgálja meg a konvergenciát.

D 1) : az integrál divergál.

Tehát az integrál -ban konvergál, -ban divergál. D

2. Newton-Leibniz formula a második típusú nem megfelelő integrálhoz

Legyen a függvény f(x) definiált és folytonos a [ a;b) és a pont közelében b a funkció korlátlan ( b- a függvény szinguláris pontja f(x)). Aztán azért f(x) ebben az intervallumban van egy antiderivált F(x) És " h>0 a rendelkezésünkre álló Newton-Leibniz képlet szerint

Ebből következik, hogy az (1) nem megfelelő integrál akkor és csak akkor létezik, ha van véges határ. Ebben az esetben a függvény F(x) folyamatos a [ a;b]. Ezután áthaladva (2) a határértékig h®0, megkapjuk a Newton-Leibniz formulát a második típusú nem megfelelő integrálhoz

Így, a második típusú nem megfelelő integrálok kiszámításához használhatja a Newton-Leibniz képletet, ha a függvény F(x) folyamatos a [ a;b] És F¢(x)=f(x) minden olyan ponton, ahol f(x) véges.

2. példa Kiszámítja.

D x=0 – speciális pont. Az antiderivált [-1;27]-en folyamatos, beleértve a pontot is x=0, ezért alkalmazhatjuk a Newton-Leibniz képletet:

3. példa Vizsgálja meg a konvergenciát.

D x=0 – speciális pont. Az antiderivatív a ponton x=0 végtelen rés. Ezért ez az integrál divergál és egyenlő ¥-vel.

jegyzet, hogy ha ezt figyelmen kívül hagyjuk és formálisan alkalmazzuk a Newton-Leibniz formulát, akkor azt kapjuk helytelen eredmény:

3. A második típusú nem megfelelő integrálok nemnegatív függvényekhez

1. tétel. Hadd f(x)³0 a [ a;b) és integrálható a [ a;b-h] "h>0. Ahhoz, hogy az (1) nem megfelelő integrál konvergáljon, szükséges és elegendő, hogy az integrálok halmaza ( h>0) felülről korlátozott. Ellenkező esetben az (1) integrál eltér, és egyenlő ¥-vel.

A második típusú nem megfelelő integrálokra, valamint az első típusú nem megfelelő integrálokra érvényes a 2. és a 3. összehasonlító tétel. Fogalmazzuk meg őket bizonyítás nélkül.

2. tétel. Hagyjuk a függvényeket fÉs g nem negatív a [ a;b) és integrálható a [ a;b-h] "h>0. Engedd tovább [ a;b) Kész

Ekkor: 1) az integrál konvergenciájából következik az integrál konvergenciája;

2) az integrál divergenciájából következik az integrál divergenciája.

3. tétel. Hagyjuk a függvényeket fÉs g nem negatív a [ a;b) és integrálható a [ a;b-h] "h>0. Ha létezik (0£ k£¥), akkor

1) az at integrál konvergenciájából k<¥ следует сходимость интеграла ,

2) az at integrál divergenciájából k>0 követi az integrál divergenciáját.

Megjegyzés. Ha a 3 0. Tétel feltételei mellett<k< ¥ (0-val nem egyenlő véges szám), akkor az integrálok egyszerre konvergálnak vagy divergálnak.

Kényelmes a teljesítményfüggvényeket összehasonlító függvénynek venni: a [ a;b) és a ( a;b] . A megfelelő integrálok konvergálnak és térnek el (ez könnyen ellenőrizhető, ha a jelzett integrálokat redukáljuk a változó lineáris változtatásával az 1. példában vizsgált integrálra).

4. példa Vizsgálja meg a konvergenciát. .

Konvergál. Ez azt jelenti, a 3. Tétel szerint, és konvergál. D

6. példa. Vizsgálja meg a konvergenciát.

D x=0 – a függvény szinguláris pontja f(x)=ln x. Hadd .

Ez többek között akkor fordul elő, amikor a<1, когда сходится. Значит, по теореме 3 сходится и данный интеграл. D

24. előadás HELYTELEN INTEGRÁLOK

Terv:

  1. A nem megfelelő integrál fogalma
  2. Az első típusú nem megfelelő integrálok.
  3. A második típusú nem megfelelő integrálok.
  1. A nem megfelelő integrál fogalma

Vegyük fontolóra mindkét típusú nem megfelelő integrál megtalálását.

Legyen adott a függvény y=f(x), folyamatos a [ a;+∞). Ha van véges határ, akkor azt hívják az első típusú helytelen integrál és jelölje.

konvergál eltér .

Az első típusú nem megfelelő integrál geometriai jelentése a következő: ha konvergál (feltéve, hogy f(x)≥0), akkor ez egy „végtelen hosszú” ívelt trapéz területét jelenti (24.1. ábra).

Hasonlóképpen egy végtelen alsó integrációs határral rendelkező helytelen integrál fogalmát vezetjük be a ( -∞ ;b] függvények: = .

A két végtelen integrációs korláttal rendelkező nem megfelelő integrált a következő képlet határozza meg: = + , ahol Val vel– tetszőleges szám.

Nézzünk példákat az első típusú nem megfelelő integrálok megtalálására.

24.1. példa.

Megoldás. Egy folytonos függvény végtelen felső határával rendelkező nem megfelelő integrál kereséséhez a következő képletet használjuk: = . Akkor = . Először is számítsuk ki az integrált e x:

= = = =∞. Azt találtuk, hogy a nem megfelelő integrál eltér.

Válasz: eltér.

Példa 24.2. Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját: .

Megoldás. Az integrandus folytonos a ( -∞ ;- 1]. Egy végtelen alsó korláttal rendelkező első típusú nem megfelelő integrál kereséséhez a következő képletet használjuk: = . Akkor = . Számítsuk ki a határjel alatti integrált: = . Szabaduljunk meg a mínusz jeltől az integráció határainak felcserélésével:

1. Azt találtuk, hogy a vizsgált nem megfelelő integrál konvergál.

Válasz: =1.

  1. A második típusú nem megfelelő integrálok.

Legyen adott a függvény y=f(x), folyamatos a [ a;b). Hadd b– a második típusú megszakítási pont. Ha van véges határ, akkor azt hívják a második típusú helytelen integrál és jelölje.



Így definíció szerint = .

Ha a talált határ egy véges számmal egyenlő, akkor a nem megfelelő integrált ennek mondjuk konvergál . Ha a megadott határérték nem létezik, vagy végtelen, akkor az integrált annak mondjuk eltér .

A második típusú nem megfelelő integrál geometriai jelentése, Ahol b– a második típusú megszakítási pont, f(x)≥0, a következő: ha konvergál, akkor egy „végtelenül magas” ívelt trapéz területét reprezentálja (24.2. ábra).

Hasonlóképpen bevezetjük a második típusú nem megfelelő integrál fogalmát a ( a;b]függvények feltéve, hogy A– a második típusú megszakítási pont: = .

24.3. példa. Számítsa ki a második típusú nem megfelelő integrált: .

Megoldás. Az integrandus folytonos a (0;1] intervallumon, és x= 0 - a második típusú szakadási pont (). A nem megfelelő integrál kiszámításához a következő képletet használjuk: =. Ezt értjük

= = = = = = = ∞. Látjuk, hogy a második fajta nem megfelelő integrálja eltér.

Válasz: eltér.

Ellenőrző kérdések:

  1. Hogyan nevezzük a nem megfelelő integrált?
  2. Milyen integrálokat nevezünk első típusú nem megfelelő integráloknak?
  3. Mi a geometriai jelentése az első típusú nem megfelelő integrálnak?
  4. Mely nem megfelelő integrálokat nevezzük konvergensnek és melyiket divergensnek?
  5. Milyen integrálokat nevezünk második típusú nem megfelelő integráloknak?
  6. Mi a geometriai jelentése egy második típusú nem megfelelő integrálnak?

BIBLIOGRÁFIA:

1. Abdrahmanova I.V. A felsőbb matematika elemei: tankönyv. kézikönyv – M.: Intenzív Oktatási Technológiák Központja, 2003. – 186 p.

2. Algebra és az elemzés kezdetei (1. rész, 2. rész): Tankönyv középfokú oktatási intézmények számára / szerk. G.N.Jakovleva. – M.: Nauka, 1981.

3. Aleksandrova N.V. Matematikai kifejezések. Címtár.- M.: Felső. iskola, 1978. - 190 p.

4. Valutse I.I., Diligul G.D. Matematika középiskolai alapú technikumoknak: Proc. juttatás. – M.: Nauka, 1989. – 576 p.

5. Grigorjev V.P., Dubinszkij Yu.A. A felsőbb matematika elemei: Tankönyv. diákoknak szakoktatási intézmények. - M.: "Akadémia" Kiadó, 2004. – 320 p.

6. Lisichkin V.T., Soloveicchik I.L. Matematika: tankönyv. kézikönyv műszaki iskolák számára. – M.: Feljebb. iskola, 1991. – 480 p.

7. Lukankin G.L., Martynov N.N., Shadrin G.A., Jakovlev G.N. Felsőfokú matematika: tankönyv. kézikönyv pedagógushallgatók számára. intézmények. – M.: Nevelés, 1988. – 431 p.

8. Írásbeli D.T. Előadásjegyzet a felsőbb matematikáról: 1. rész. – M.:Iris-press, 2006.- 288 p.

9. Filimonova E.V. Matematika: tankönyv. kollégiumi juttatás. – Rostov n/d: Főnix, 2003. – 384 p.

10. Shipachev V.S. Felsőfokú matematika: tankönyv egyetemek számára. – M.: Felsőiskola, 2003. – 479 p.

11. Shipachev V.S. Felsőfokú matematika tantárgy: felsőoktatás. – M.: PROYUL M.A. Zakharov, 2002. – 600 p.

12. Enciklopédia gyerekeknek. T.11. Matematika / Ch. szerk. M.V.Aksenova. - M.: Avanta+, 2000.- 688 p.

Nem megfelelő integrálok

Lk5,6 (4h)

A koncepciót azzal a feltételezéssel vezették be, hogy:

1) az integrációs intervallum véges (szegmens [ a;b]),

2) funkció f(x) legfeljebb [ a;b].

Az ilyen határozott integrált ún saját(a „saját” szó kimarad). Ha ezen feltételek bármelyike ​​nem teljesül, akkor a határozott integrált hívjuk nem a sajátod. Az első és a második típusú nem megfelelő integrálok vannak.

1. Az első típusú nem megfelelő integrál definíciója

Általánosítsuk a határozott integrál fogalmát egy végtelen intervallumra. Hadd f(x) a [ a;+¥) és minden véges részébe integrálható, azaz . Ebben az esetben van egy integrál. Nyilvánvaló, hogy van egy függvény definiálva a [ a;+¥). Mérlegeljük. Ez a határ lehet vagy nem létezik, de ettől függetlenül hívják az első típusú helytelen integrálés ki van jelölve.

Meghatározás. Ha létezik és véges, akkor a nem megfelelő integrált hívjuk konvergens, és ennek a határértéknek az értéke a nem megfelelő integrál értéke. . Ha nem létezik, vagy egyenlő ¥-vel, akkor a nem megfelelő integrált hívjuk meg divergens.

Hasonlóan meghatározott,

1. példa Vizsgáljuk meg a , integrál konvergenciáját.

D folyamatos a [ a;+¥) .

Ha , akkor , és Þ az integrál konvergál.

Ha , akkor az integrál eltér.

Így, konvergál a és ;

.D-nél eltér

2. Az első típusú nem megfelelő integrál tulajdonságai

Mivel a nem megfelelő integrált a Riemann-integrál határértékeként definiáljuk, így a határértékre való áthaladás során megőrzött összes tulajdonság átkerül a nem megfelelő integrálba, vagyis az 1-8. tulajdonságok teljesülnek. Az átlagérték tételnek nincs értelme.

3. Newton–Leibniz képlet

Legyen a függvény f folyamatos a [ a;+¥), F- antiderivatív és létezik. Ekkor érvényes a Newton–Leibniz képlet:

Valóban,

2. példa D. D

Az első típusú nem megfelelő integrál geometriai jelentése

Legyen a függvény f nem negatív és folyamatos a [ a;+¥) és a nem megfelelő integrál konvergál. megegyezik egy íves trapéz területével az alappal [ a;b], és egyenlő az alapterülettel [ a;+¥).

4. Nemnegatív függvények nem megfelelő integráljai

1. tétel. Hadd f(x)³0 a [ a;+¥) és integrálható a [ a;b] "b>a. Egy nem megfelelő integrál konvergenciájához szükséges és elegendő, hogy az integrálok halmaza felülről korlátos legyen, és .

Bizonyíték.

Vegye figyelembe a funkciót, a£ b. Mert f(x)³0, akkor F nem csökken Valóban, " b 1 , b 2: a£ b 1 <b 2, mivel teljesül

Definíció szerint egy nem megfelelő integrál akkor és csak akkor konvergál, ha van véges. Mert F(b) nem csökken, akkor ez a határ akkor és csak akkor áll fenn, ha a függvény F(b) felülről korlátos, azaz $ M>0: "b>a. Ahol

A nem megfelelő integrál divergenciája azt jelenti, hogy .

2. tétel. Hagyjuk a függvényeket fÉs g nem negatív a [ a;+¥) és integrálható a [ a;b] "b>a. Engedd tovább [ a;+¥) kész

1) a (2) integrál konvergenciájából a (3) integrál konvergenciája következik;

2) a (3) integrál divergenciájából a (2) integrál divergenciája következik.

Bizonyíték.

innen: (1) " b>a.

1) Konvergáljon a (2) integrál. Az 1. Tétel szerint a halmaz korlátos korlátos. Az 1. tétel szerint konvergál.

2) Hagyd, hogy szétszóródjanak. Bizonyítsuk be, hogy a (2) integrál divergál. Az ellenkezőjéből. Tegyük fel, hogy a (2) integrál konvergál, de ekkor a tétel első részével a (3) integrál konvergál - ez ellentmondás a feltétellel.

3. tétel. Hagyjuk a függvényeket fÉs g nem negatív a [ a;+¥) és integrálható a [ a;b] "b>a. Ha létezik (0£ k£¥), akkor

1) az at integrál konvergenciájából k<¥ следует сходимость интеграла ,

2) az at integrál divergenciájából k>0 követi az integrál divergenciáját.

Bizonyíték.

1) Hagyjuk k<¥ и сходится.

Mert konvergál, konvergál, azt jelenti, hogy konvergál. Ekkor a (4) értelmében konvergál. Innen konvergál.

2) Hagyjuk k>0 és eltér. Ebben az esetben - egy véges szám. Ha ennek az ellenkezőjét feltételezzük - hogy az integrál konvergál, akkor az 1) bekezdésben igazolva azt találjuk, hogy ez is konvergál, és ez ellentmond a feltételnek. Ezért a feltevés helytelen és eltérő. abszolút konvergál, akkor definíció szerint konvergál. Szóval belefér. De belefér.

Itt vagy most? =) Nem, nem akartam megfélemlíteni senkit, csak a helytelen integrálok témaköre nagyon jól mutatja, mennyire fontos, hogy ne hanyagoljuk el a felsőbb matematikát és egyéb egzakt tudományokat. A weboldalon minden megtalálható, ami a lecke elsajátításához szükséges - igény szerint részletes és hozzáférhető formában...

Tehát kezdjük azzal. Képletesen szólva a nem megfelelő integrál egy „fejlett” határozott integrál, és valójában nincs is velük olyan sok nehézség, ráadásul a nem megfelelő integrálnak nagyon jó geometriai jelentése van.

Mit jelent egy nem megfelelő integrál értékelése?

Számítsa ki a helytelen integrált - ez a SZÁM megtalálását jelenti(pontosan ugyanaz, mint a határozott integrálban), vagy bebizonyítani, hogy eltér(vagyis szám helyett a végtelent kapod).

Kétféle nem megfelelő integrál létezik.

Nem megfelelő integrál végtelen integrációs korláttal

Néha egy ilyen helytelen integrált hívnak az első típusú helytelen integrál. Általánosságban elmondható, hogy a végtelen határértékkel rendelkező nem megfelelő integrál leggyakrabban így néz ki: . Miben különbözik a határozott integráltól? A felső határon. Végtelen: .

Ritkábban fordulnak elő a végtelen alsó határértékkel vagy két végtelen határértékkel rendelkező integrálok: , majd később megnézzük őket - ha ráérsz :)

Nos, most nézzük a legnépszerűbb esetet. A példák túlnyomó többségében az integrand függvény folyamatos között, és ez fontos tényt először ellenőrizni kell! Mert ha vannak hiányosságok, akkor vannak további árnyalatok. A határozottság kedvéért tegyük fel, hogy akkor is a tipikus ívelt trapézígy fog kinézni:


Figyeljük meg, hogy végtelen (jobb oldalon nincs korlátos), és helytelen integrál számszerűen megegyezik a területével. A következő lehetőségek lehetségesek:

1) Az első gondolat, ami eszünkbe jut: „mivel az alak végtelen, akkor ", vagyis a terület is végtelen. Lehet, hogy így van. Ebben az esetben azt mondják, hogy a nem megfelelő integrál eltér.

2) De. Bármilyen paradoxon is hangzik, egy végtelen alak területe egyenlő lehet... egy véges számmal! Például: . Ez igaz lehet? Könnyen. A második esetben a nem megfelelő integrál konvergál.

3) A harmadik lehetőségről kicsit később.

Milyen esetekben divergál és milyen esetekben konvergál egy nem megfelelő integrál? Ez az integrandustól függ, és hamarosan konkrét példákat is megvizsgálunk.

Mi történik, ha egy végtelen görbe trapéz található a tengely alatt? Ebben az esetben a nem megfelelő integrál (eltér) vagy egyenlő egy véges negatív számmal.

És így, a nem megfelelő integrál lehet negatív.

Fontos! Ha BÁRMILYEN helytelen integrált megoldásra kapsz, akkor általában véve nincs szó semmilyen területről és nem kell rajzot építeni. A nem megfelelő integrál geometriai jelentését csak az anyag megértésének megkönnyítése érdekében magyaráztam el.

Mivel a nem megfelelő integrál nagyon hasonlít a határozott integrálhoz, emlékezzünk a Newton-Leibniz képletre: . Valójában a képlet nem megfelelő integrálokra is alkalmazható, csak kicsit módosítani kell. Mi a különbség? Az integráció végtelen felső határán: . Valószínűleg sokan sejtették, hogy ez már a határok elméletének alkalmazására utal, és a képlet így lesz írva: .

Mi a különbség a határozott integráltól? Semmi különös! A határozott integrálhoz hasonlóan meg kell tudni találni az antiderivatív függvényt (határozatlan integrál), és tudnia kell alkalmazni a Newton-Leibniz formulát. Az egyetlen dolog, ami hozzáadásra került, az a határérték kiszámítása. Akinek rossz dolga van velük, vegye le a leckét Funkciókorlátok. Példák megoldásokra, mert jobb későn, mint a hadseregben.

Nézzünk két klasszikus példát:

1. példa

Az egyértelműség kedvéért rajzolok egy rajzot, bár még egyszer hangsúlyozom, gyakorlaton Ebben a feladatban nincs szükség rajzok készítésére.

Az integráns függvény a félintervallumon folyamatos, ami azt jelenti, hogy minden rendben van, és a nem megfelelő integrál kiszámítható a „standard” módszerrel.

Képletünk alkalmazása és a probléma megoldása így néz ki:

Vagyis a nem megfelelő integrál eltér, és az árnyékolt ívelt trapéz területe egyenlő a végtelennel.

A vizsgált példában a legegyszerűbb táblázatintegrált használjuk, és ugyanazt a technikát alkalmazzuk a Newton-Leibniz-formula alkalmazására, mint a határozott integrálban. De ezt a képletet a határ jele alatt alkalmazzuk. A „dinamikus” változó szokásos betűje helyett a „be” betű jelenik meg. Ennek nem szabad megzavarnia vagy megzavarnia, mert egyik betű sem rosszabb, mint a szabványos „X”.

Ha nem érti, hogy miért pontban, akkor ez nagyon rossz, vagy nem érti a legegyszerűbb határértékeket (és általában nem érti, mi az a határ), vagy nem tudja, hogy néz ki egy logaritmikus függvény grafikonja. A második esetben vegyen részt egy leckében Elemi függvények grafikonjai és tulajdonságai.

A nem megfelelő integrálok megoldásánál nagyon fontos tudni, hogyan néznek ki az alapvető elemi függvények grafikonjai!

A kész feladatnak valahogy így kell kinéznie:

“

! Példa készítésekor mindig megszakítjuk a megoldást, és jelezzük, hogy mi történik az integrandusszal – folyamatos az integráció intervallumán vagy sem?. Ezzel azonosítjuk a nem megfelelő integrál típusát, és indokoljuk a további lépéseket.

2. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Készítsük el a rajzot:

Először is megjegyezzük a következőket: az integrandus a félintervallumon folytonos. Kapucni. A képlet segítségével oldjuk meg :

(1) Vegyük egy hatványfüggvény legegyszerűbb integrálját (ez a speciális eset sok táblázatban megtalálható). Jobb, ha a mínusz jelet azonnal a határjelen túlra mozgatja, hogy ne akadályozza a további számításokat.

(2) A felső és alsó határt a Newton-Leibniz képlet segítségével helyettesítjük.

(3) Jelezzük, hogy (Uraim, ezt már régen érteni kellett volna), és leegyszerűsítjük a választ.

Itt egy végtelen görbe trapéz területe véges szám! Hihetetlen, de igaz.

A kész példának valahogy így kell kinéznie:

“

Az integrand függvény folyamatosan be van kapcsolva

“

Mi a teendő, ha olyan integrállal találkozik, mint - -val töréspont az integrációs intervallumon? Ez azt jelenti, hogy a példában elírás van. (Legvalószínűbb), vagy emelt szintű képzésről. Ez utóbbi esetben azért additív tulajdonságok, figyelembe kell venni két helytelen integrált intervallumokon, majd kezelni az összeget.

Néha elírás vagy szándékosság miatt előfordulhat, hogy egy nem megfelelő integrál egyáltalán nem léteznek, tehát ha például az „x” négyzetgyökét a fenti integrál nevezőjébe helyezzük, akkor az integrációs intervallum egy része egyáltalán nem fog szerepelni az integrandus definíciós tartományában.

Sőt, előfordulhat, hogy a nem megfelelő integrál még a „látszólagos jóllét” ellenére sem létezik. Klasszikus példa: . A koszinusz határozottsága és folytonossága ellenére ilyen nem megfelelő integrál nem létezik! Miért? Nagyon egyszerű, mert:
- nem létezik megfelelő határértéket.

És ilyen példák, bár ritkán, de előfordulnak a gyakorlatban! Így a konvergencia és a divergencia mellett van a megoldásnak egy harmadik eredménye is, amely érvényes választ ad: „nincs helytelen integrál”.

Azt is meg kell jegyezni, hogy a nem megfelelő integrál szigorú definíciója pontosan a határon keresztül van megadva, és aki szeretné, az ismerkedhet vele az oktatási szakirodalomban. Nos, folytatjuk a gyakorlati órát, és áttérünk az értelmesebb feladatokra:

3. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Először próbáljuk meg megtalálni az antiderivatív függvényt (határozatlan integrál). Ha ezt nem tesszük meg, akkor természetesen a nem megfelelő integrált sem tudjuk megoldani.

Melyik táblázatintegrálhoz hasonlít az integrandus? Arktangensre emlékeztet: . Ezek a megfontolások azt sugallják, hogy jó lenne egy négyzet a nevezőben. Ez cserével történik.

Cseréljük:

A határozatlan integrált ebben az esetben nincs értelme konstanst hozzáadni.

Mindig hasznos ellenőrizni a piszkozatot, vagyis megkülönböztetni a kapott eredményt:

Az eredeti integrált megkaptuk, ami azt jelenti, hogy a határozatlan integrált helyesen találtuk meg.

Most megtaláljuk a nem megfelelő integrált:

(1) A megoldást a képlet szerint írjuk fel . Jobb, ha az állandót azonnal a határjelen túlra mozgatjuk, hogy ne zavarja a további számításokat.

(2) A felső és alsó határértéket a Newton-Leibniz képlet szerint helyettesítjük. Miért nál nél ? Lásd az arctangens grafikont a már ajánlott cikkben.

(3) Megkapjuk a végső választ. Egy tény, amit hasznos fejből tudni.

Előfordulhat, hogy a haladók nem találják meg külön a határozatlan integrált, és nem alkalmazzák a helyettesítési módszert, hanem inkább azt a módszert használják, hogy a differenciáljel alatti függvényt behelyettesítik, és a nem megfelelő integrált „azonnal” megoldják. Ebben az esetben a megoldásnak valahogy így kell kinéznie:

“

Az integrandus folyamatos a .

“

4. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

! Ez egy tipikus példa, és nagyon gyakran találunk hasonló integrálokat. Dolgozd ki jól! Az itt található antiderivatív függvény a teljes négyzet kiválasztásának módszerével található meg a leckében Néhány tört integrálása.

5. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Ez az integrál részletesen megoldható, azaz először változó változtatással keressük meg a határozatlan integrált. Vagy "azonnal" megoldhatja - a függvényt a differenciáljel alá foglalva. Kinek van matematikai képzettsége?

Teljes megoldások és válaszok a lecke végén.

Az oldalon találhat példákat a végtelen alsó integrációs határú helytelen integrálok megoldására Hatékony módszerek a nem megfelelő integrálok megoldására. Itt azt az esetet is elemeztük, amikor az integráció mindkét határa végtelen.

Korlátlan függvények nem megfelelő integráljai

Vagy a második típusú nem megfelelő integrálok. A második típusú nem megfelelő integrálok alattomos módon a szokásos határozott integrál alá vannak „titkosítva”, és pontosan ugyanúgy néznek ki: De a határozott integrállal ellentétben az integrandus végtelen folytonossági hiányt szenved (nem létezik): 1) a pontban, 2) ill. pontban, 3) vagy mindkét pontban egyszerre, 4) vagy akár az integrációs szegmensen. Megvizsgáljuk az első két esetet a 3-4. esethez a cikk végén található egy hivatkozás egy további leckére.

Csak egy példa, hogy világos legyen: . Úgy tűnik, ez egy határozott integrál. De valójában ez a második típusú nem megfelelő integrál, ha az alsó határ értékét behelyettesítjük az integrandusba, akkor a nevezőnk nullára megy, vagyis az integrandus ezen a ponton egyszerűen nem létezik!

Általában egy nem megfelelő integrál elemzésekor mindig mindkét integrációs korlátot be kell cserélnie az integrandusba. Ezzel kapcsolatban nézzük meg a felső határt: . Itt minden rendben van.

A vizsgált nem megfelelő integráltípus görbe trapézja alapvetően így néz ki:

Itt minden majdnem ugyanaz, mint az első típusú integrálban.

Integrálunk numerikusan egyenlő az árnyékolt íves trapéz területével, amely felülről nincs határolva. Ebben az esetben két lehetőség lehet*: a nem megfelelő integrál divergál (a terület végtelen), vagy a nem megfelelő integrál egy véges számmal (vagyis egy végtelen alak területe véges!).

* alapértelmezés szerint általában azt feltételezzük, hogy létezik a nem megfelelő integrál

Már csak a Newton-Leibniz képlet módosítása van hátra. Határ segítségével is módosul, de a határ már nem a végtelen felé hajlik, hanem a jobb oldali értékre. A rajzból könnyen követhető: a tengely mentén végtelenül közel kell megközelíteni a töréspontot jobb oldalon.

Lássuk, hogyan valósul meg ez a gyakorlatban.

6. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Az integrandusnak végtelen a folytonossági hiánya egy ponton (ne felejtse el szóban vagy piszkozaton ellenőrizni, hogy minden rendben van-e a felső határértékkel!)

Először is számítsuk ki a határozatlan integrált:

Csere:

Ha nehézségei vannak a cserével kapcsolatban, kérjük, olvassa el a leckét Behelyettesítési módszer határozatlan integrálban.

Számítsuk ki a nem megfelelő integrált:

(1) Mi újság itt? Megoldástechnika terén gyakorlatilag semmi. Csak a limit ikon alatti bejegyzés változott: . Az összeadás azt jelenti, hogy a jobb oldali értékre törekszünk (ami logikus – lásd a grafikont). Az ilyen határt a határok elméletében ún egyoldalú határ. Ebben az esetben van jobb oldali határ.

(2) A felső és alsó határt a Newton-Leibniz képlet segítségével helyettesítjük.

(3) Foglalkozzunk a következővel: . Hogyan határozható meg, hogy egy kifejezés hova megy? Durván fogalmazva, csak be kell cserélni az értéket, be kell cserélni háromnegyedet, és jelezni kell, hogy . Fésüljük át a választ.

Ebben az esetben a nem megfelelő integrál egyenlő egy negatív számmal. Ebben nincs bűnözés, csak a megfelelő íves trapéz található a tengely alatt.

És most két példa a független megoldásokra.

7. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

8. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Ha az integrandus nem létezik a ponton

Egy ilyen helytelen integrálhoz tartozó végtelen görbe trapéz alapvetően így néz ki.